Harmonie není náhoda IV - durová stupnice pod mikroskopem
Durová stupnice pod mikroskopem
Osvěžme si, jak se k přirozené durové stupnici dospěje. Ke zvolenému základnímu tónu přidáme dalších pět vyšších tónů, které kmitají dvakrát, třikrát... až šestkrát rychleji. Té řadě říkejme tónika. Pak utvoříme další podobné řady: dominantu, která kmitá o polovinu rychleji než tónika, a subdominantu, jež kmitá o třetinu rychleji než tónika. Takto vzniklé tóny dají dohromady durovou stupnici v rozsahu třetí oktávy nad základním tónem. Je-li základním tónem velké C, dostali jsme stupnici C dur v rozsahu jednočárkové oktávy.
Horní tři tóny v každé z těchto tří řad tvoří trojzvuk zvaný kvitakord s poměrem kmitočtů 4 : 5 : 6.
Jak osvěžit harmonii
Na hotové stupnici se uvažovaný trojzvuk jeví "ob stupeň" postavený na I., IV. nebo V. stupni. Proč byste, hudebníci, nezkusili něco podobného postavit na ostatních stupních? Vedlejší kvintakord na III. stupni bude mollový, který, podle obrázku 8, má vespod tercii malou z horní poloviny kvintakrodu T a nahoře má tercii velkou z dolní poloviny kvintakordu D. Je tedy intervalově obrácený než durový a poměr kmitočtů je 10 : 12 : 15. Že bude znít příjemně, konsonantně, to naznačíme příště také početním přístupem. Podobně lze vytvořit mollový akord na VI. stupni ze S a T, avšak na II. stupni takové odvození není možné, protože pro spodní malou tercii nemáme k dispozici žádnou hotovou harmonickou funkci.
Durová stupnice v číslech
Podívejme se proto podrobněji na intervaly ve stupnici. Zjistíme, že i v běžných pojmech jako je celý tón nebo půltón, budeme muset být přesnější, než je zvykem.

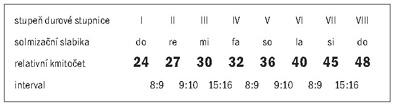
Nejprve hledejme nejmenší celá čísla, která vyjádří stupnici v poměrných kmitočtech. Čísla budou v rozsahu: 4 až 8 (třetí oktáva nad základním tónem) krát 2 (po odstranění polovin v D) krát 3 (po odstranění třetin v S), a to se rovná 24 až 48.
Když si prohlédnete tabulku na obrázku 9, najdete tam zajímavá čísla charakterizující opravdu přirozenou čistou durovou stupnici ("podle Zarlina"). Sousední tóny tvoří tři různé intervaly: za prvé 8 : 9 zvaný velký celý tón, za druhé 9 : 10 zvaný malý celý tón. Jejich poměr je 80 : 81, odborníky nazývaný schizma, což znamená rozštěpení. Třetí interval je 15 : 16, velký půltón. Podívejme se ještě, jak se liší velká a malá tercie. Tedy (4 : 5) : (5 : 6) = 24 : 25. Nazývá se malý půltón.
Za hranicí ideálu
Máme dva trochu odlišné celé tóny, dva odlišné půltóny. Shodují se jen v tom, že velký a malý půltón dají dohromady malý celý tón. Čisté ladění v detailech už nevypadá tak jednoduše, protože přirozené stupnice nemívají stejně velké stupně.
Teď se také můžeme podívat, jak dopadne pokus o mollový kvintakord na II. stupni. Krajní tóny mají poměr kmitočtů 27 : 40, což není přesně 2 : 3, ta čísla neodpovídají čisté kvintě. II. stupeň je o schizma výš, než by se nám hodilo. Tentýž tón způsobuje malý rozdíl mezi spodním a horním tetrachordem, mezi dolní a horní půlkou stupnice.
Ideální řešení tohoto zádrhelu neexistuje, spíš se malý rozdíl mezi velkým a malým celým tónem zanedbává. Je také možno II. stupeň snížit, abychom dostali čistý mollový kvintakord na II. stupni a měli oba tetrachordy stejné, jak navrhoval stupnici Cartesius.
V praktických učebnicích hudby se takové podrobnosti neuvádějí, ale my teď víme, že stejný tón může znít v jedné souvislosti úplně čistě a v jiné souvislosti už ne tak docela čistě. Je vlastností veškerých složitějších jevů, že nejsou ideální ve všech situacích.
Milí čtenáři, v této čtvrté části jsme se zaměřili na detaily v durové stupnici, a teď jsme vybaveni, abychom se příště mohli fundovaně a velkoryseji vrhnout na matematické odvození mollového kvintakordu.