Rockové klávesy - Fibonacciho posloupnost a zlatý řez v hudbě

Fibonacci Series and the Golden Ratio in Music
Welcome readers! After a few months of very technical articles, I wanted to shake things up a bit with a more conceptual one. I have always been fascinated by mathematics and patterns in music. On my own, I have been studying a lot of different schools of mathematics lately. The deeper I go with my studies, the more I am convinced that music, and all life for that matter, is controlled by a kind of “sacred math”. I wanted to focus this month on two specific concepts, The Fibonacci sequence and the golden ratio. In a way, they are actually one thing, as you will see because both concepts are expressed within each other. These ideas directly impact the rules of Western music. You could even say they ARE the rules. This investigation will be a two-part article; this month I will cover the theory. Next month I’ll give lots of musical examples and give you tools to use these concepts in your own music. This is a very advanced topic so try to read the material slowly and give it time to sink in. I’ve tried to simply the equations and explanations as much as possible also. Let’s start with a little history lesson.
The Fibonacci Sequence
Leonardo of Pisa (1170-1240), known mostly by his nickname, Fibonacci, is considered by many to be the first important European mathematician. On his many trips to Byzantium and Africa, Leonardo learned much about Arabic mathematics, which was, at the time, far superior to that of Europe. In his book, Liber Abaci, or Book of the Abacus published in 1202, Leonardo combined his own theories with the Arabic math that he learned. The book was the major reason Europe adopted the Arabic number system and was, for many years, the most important math text in Europe. In Fibonacci’s groundbreaking work, there is a whimsical word problem that illustrates what would later be known as the Fibonacci sequence.
Leonardo’s Rabbits
Leonardo posed the following question: “How many pairs of rabbits would result from one original pair of fertile rabbits after the original pair and offspring mated for one year?” He assumed that each pair would produce another pair of each sex that would be fertile two months after birth. After one month there are two pairs of rabbits, the original pair and the pair that is their offspring. The next month the first offspring is still not fertile and the original pair has had another pair of rabbits which makes three pairs total. In the 3rd month two pairs of the rabbits are fertile and one is not so two new pairs are added to the existing three making five pairs of rabbits. This pattern is the called the Fibonacci sequence.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.
The sequence can also be analyzed as adding the new number to the number that came just before in the sequence. 1 + 1 = 2, 2 + 1 = 3 , 3 + 2 = 5, etc.
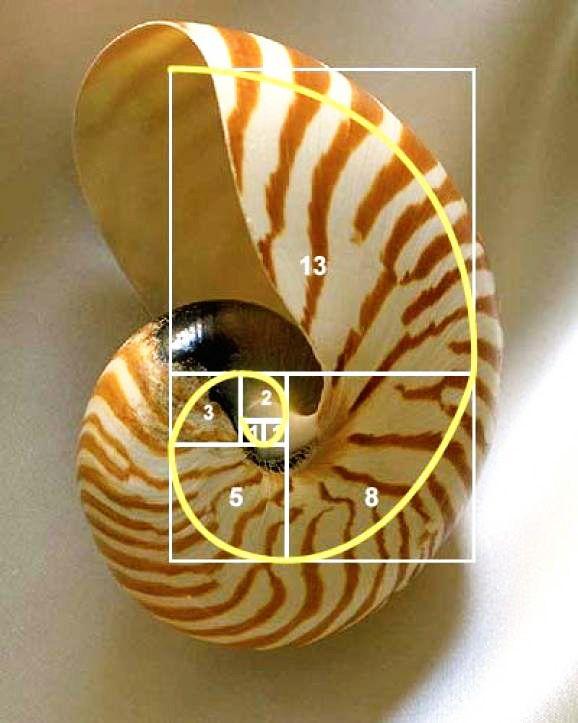
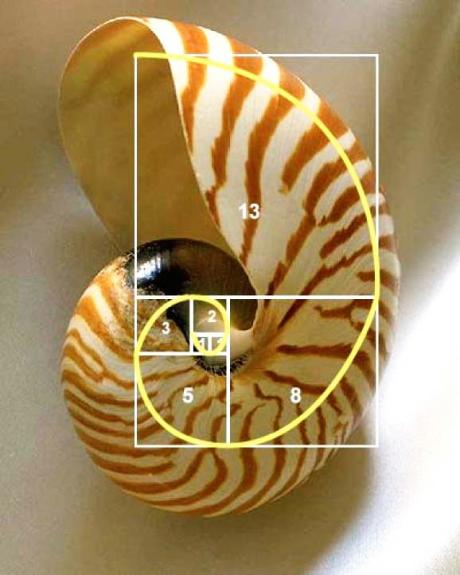
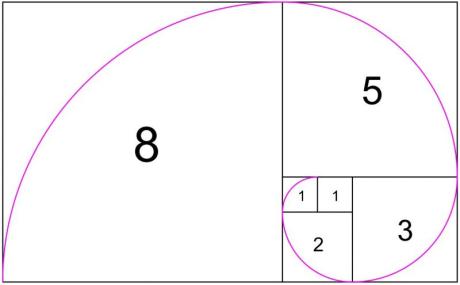
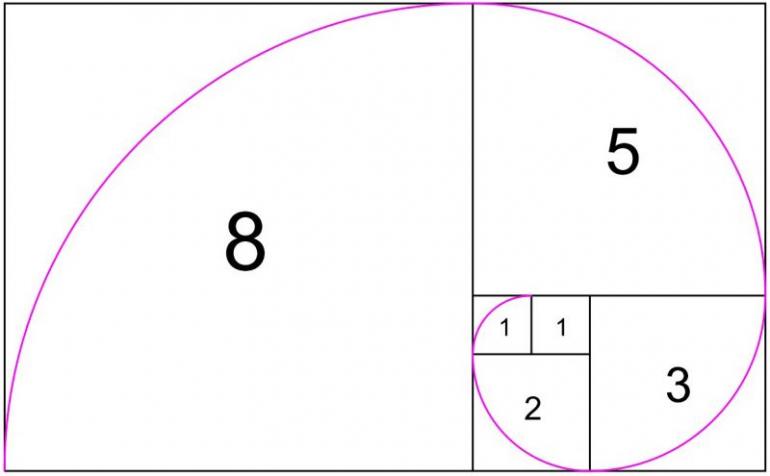
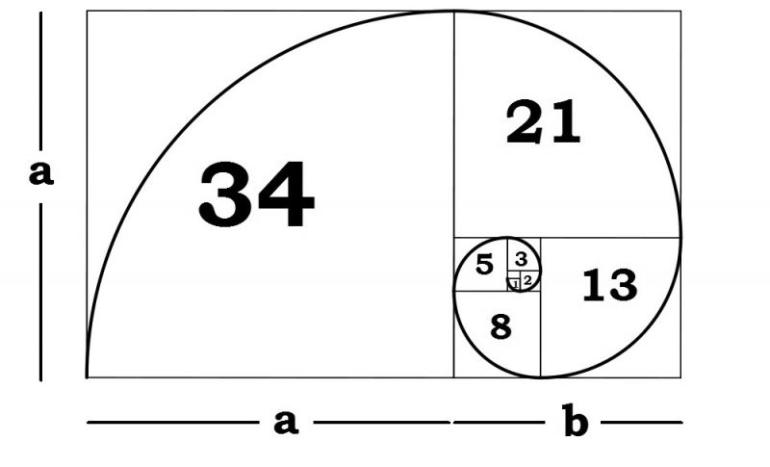
The interesting thing about the Fibonacci sequence is how much it appears in nature, art, and music. Take a look at Image 1. This graphic illustrates the Fibonacci series as a set of geometric shapes. We construct a square whose sides measure 1. Beside it we put another square of the same size in keeping with the sequence. We then attach another square that has the length 2 (adding the two previous numbers). We add the longest side or 1 + 2 to get a square with a length of the side 3 to this square and so on. This continues in the process seen in Image 1. If we draw a quadrant in each square we get what is know as the Fibonacci spiral. This spiral can be seen everywhere in the world. Sea shells, sunflowers, and great works of art. All have this “sacred” geometry running through them. The Fibonacci Spiral is a system of organic growth that retains balance throughout the process. In art and music it’s also associated with a feeling of harmony and beauty. This magical mathematical principle is the reason why trees don’t tip over as they grow. If you look at the artichoke you can also see the pattern; on the outside there are 8 rows of “vertical” leaves that also form a “horizontal” pattern of 5. When we see consecutive Fibonacci numbers, such as this 5:8 ratio of the artichoke, we can assume that our sacred geometry is at work. Take a look at a few examples of the Fibonacci Spiral.
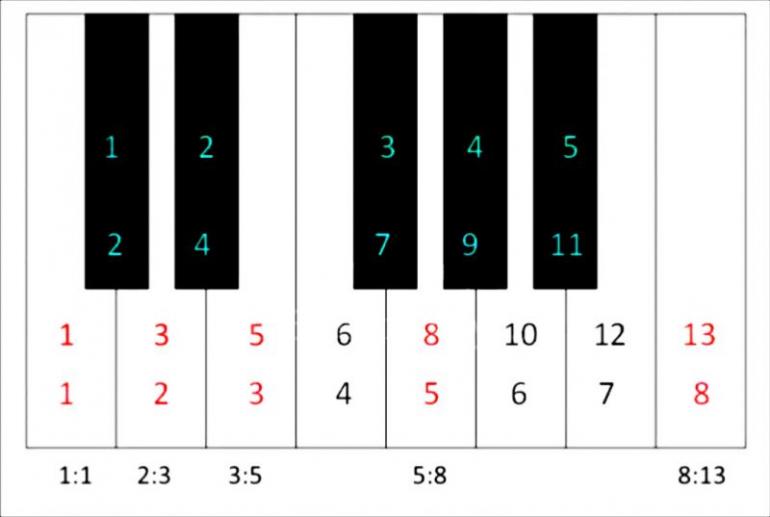
Fibonacci Series in the Piano Keyboard
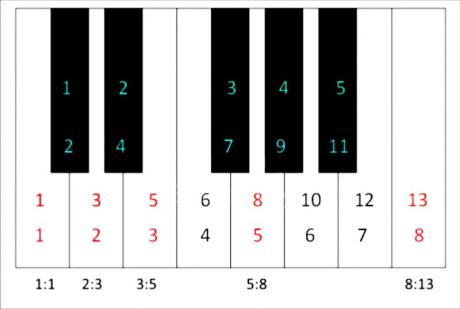
The magic of the Fibonacci numbers can clearly be seen on the piano keyboard. Take a look at Image 6. We see that in every octave on the piano there are 8 white keys and 5 black keys; sound familiar? If we count all the keys in the chromatic scale and overlay those numbers on the white keys, we see many consecutive Fibonacci relationships; 1 : 1 on C, 2 : 3 on D, 3 : 5 on E, 5 : 8 on G, 8 : 13 on octave C. Many people believe that our system of music in the West sounds so balanced, harmonious, and beautiful because of this Fibonacci balance.

The Golden Ratio
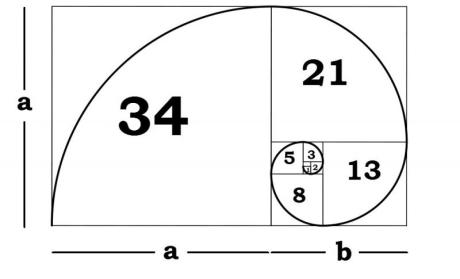
A concept very closely related to the Fibonacci Series is what is known as the golden ratio. This concept was discovered by the Greek “father of geometry”, Euclid, in 300 BC. The golden ratio is a special number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part (a + b is to a as a is to b). It is often symbolized using the Greek character, phi. It’s number equivalent is an irrational number that is usually abbreviated as 1.618. Johannes Kepler in 1600 discovered the relationship between the Fibonacci Spiral and the Golden Ratio. Take a look at image 8 and notice that the Golden Ratio has been added to our Fibonacci Squares. The proportions are the same! To further prove this point, notice that as the Fibonacci numbers grow in size and are divided by the number that came just before in the sequence we get closer and closer to the numeric figure of phi (1.618.....). If we try this calculation with the 19th and 20th numbers of the sequence (9349 and 15127) we get the following equation 15.127/9349 = 1.618034. This is exactly the golden ratio to the 6th decimal.
Use of the golden ratio by Bach
Let’s see these concepts at work in a very famous piece of music, Bach’s 1st Prelude in C from Well Tempered Klavier. Here’s a link to the music.
The piece is 35 measures long. At bar 21, Bach uses a very unusual F# Diminished chord which provides the highest degree of tension in the piece. Let’s use the following equation to see if measure 21 is the “Golden Measure”. We can use the following equation to figure this out in any piece of music;
N x .618 = the Golden Measure
where N = the number of measures and .618 is the inverse of phi
35 x .618 = 21.63
As you can see, Bach uses the golden ratio numbers to select the location of the most dramatic tension of the piece. Remember that these numbers are associated with balance and harmony so it’s not surprising that great composers use them with great effect in their music. Composers like Bach and Beethoven were also quite probably members of the secret Masonic Order. It’s greatly believed that this sacred Math was some of the most closely guarded secrets of the early Masons.
Next month we will take a look at other composers like Bartok and Beethoven to see how they used these magical number systems. I’ll give you some techniques to use these ideas in your own rock keyboard parts and songs as well.