Zkreslení z Moravy - výrobní reportáž

Simulace kytarových aparátů a krabiček, a vlastně simulace vůbec, už tu s námi jsou hezkých pár let. Někteří je bez výčitek používají a obdivují, jiní je naopak neuznávají a zarputile je zatracují. Nicméně, ať už ti nebo oni, ne všichni ví, co stálo za jejich zrodem a na jakých principech simulace vlastně pracují.
Podobná úvaha utkvěla v hlavě i nám, a tak jsme využili příležitosti dozvědět se něco více o jejich vývoji. Vypravili jsme se tedy pohodlným vlakem EC 275 Jaroslav Hašek napříč republikou do brněnské firmy Audiffex, kde jsme se setkali přímo s tvůrci tuzemských simulací, Jaromírem Mačákem a Luborem Přikrylem. Náš rozhovor začal zcela spontánně už cestou od vlaku a tak trochu „odprostředka“ - debatou o převodnících a dynamice. Vstupme do něj tedy ze stejného místa...
Je nějaký požadavek na vstupní převodníky z hlediska speciálnosti hudebních nástrojů, konkrétně hlavně kytary?
Nemyslím si, je to naprosto standardní studiová věc. Pouze je nutné použít převodník s vysokou vstupní impedancí, abych nezatěžoval snímač kytary. Řada lidí se snaží hrát přes software a diví se, že jim to nehraje, když to mají zapojené do klasického vstupu zvukové karty. Pokud nemám vysokoimpedanční vstup přímo na kartě, musím mít nějaký předzesilovač nebo zařízení, které mi to zajistí. Jinak bych řekl, že zrovna u kytary jsou převodníky možná trochu přeceňovaným faktorem vzhledem k jejímu frekvenčnímu rozsahu. Podle mě je nezbytné mít dobrý odstup signálu od šumu. Když se budeme bavit o zkreslovačích, tak ty udělají v principu to, že vstupní signál mnohonásobně zesílí a potom ho nějakým způsobem „ořežou“. Pokud mám na vstupním převodníku nějaký šum, nechci teď říkat nějaké konkrétní hodnoty, tak po zesílení budu mít na výstupu samozřejmě mnohonásobně zesílený i ten šum. Ořezáním ale změním jeho poměr vůči užitečnému signálu a šum se pak, bohužel, projeví mnohem více.
Zajímavé je, že většina lidí v souvislosti s převodníky řeší spíš dynamiku než šum...
O tom vím, ale podle mě u převodníku problém s dynamikou určitě není. Vezmi si, že dnes se převodníky dělají standardně čtyřiadvacetibitové, takže máš k dispozici 224 (16 772 216) hodnot. Například z kytarového snímače jde řekněme ±300 mV, které lze rozdělit na necelých sedmnáct miliónů úrovní. To je dostatečně jemná škála k pokrytí celé úrovně signálu. Ale hlavně je to důležité pro ten odstup signálu od šumu. Zjednodušeně se dá říct, že každý bit navíc zvyšuje odstup šumu o zhruba 6 dB.
Převodníky tedy nevyvíjíš. Už dostaneš nějaký hotový a ten použiješ?
Řekl bych to možná trochu jinak. Ty systémy jsou v podstatě dva. Jeden je klasické PC, kde je tohle všechno vyřešené pomocí zvukové karty, tam se o to hardwarové propojení nemusíme starat. Druhá možnost je vyvíjet vlastní hardware, kde si musíme naopak všechno řešit sami, tj. procesor, vyrovnávací paměti, převodníky atd. Já osobně se zabývám většinou implementací nějakého algoritmu na konkrétním procesoru. O ty hardwarové věci se až tak starat nemusím.
Dobře, mám tedy jack z kytary zapojený do správného vstupu, co se děje dál?
Signál z kytary mi převodník navzorkuje. To znamená, že v příslušné vzorkovací frekvenci (např. 48tisíckrát za vteřinu) mi v každý okamžik odečte úroveň vstupního signálu a převede ji na číslo v digitální formě. Na to jsou dva pohledy. Jeden je, jak je to skutečně uložené přímo v procesoru, tedy sled nul a jedniček. Ovšem to není zrovna lidský formát.
Při programování proto používáme druhý přístup a využíváme různé tzv. datové typy. Nejčastěji používáme celočíselné datové typy a nebo čísla s tzv. plovoucí řádovou čárkou, což je reprezentace reálných čísel.
A to už je vlastně to, co já dostanu do programu. Řekněme tedy, že mám na vstupu například kontinuální střídavé napětí ±1 V. Následuje převod té vlny (vlastní digitalizace) na sled jednotlivých bitů. Pak si zvolím vhodný datový typ a ve finále +1 V vidím jako číslo 1,0 a analogicky -1 V vidím jako číslo -1,0. Takže já pak se signálem dál pracuji normálně jako s reálnými čísly.
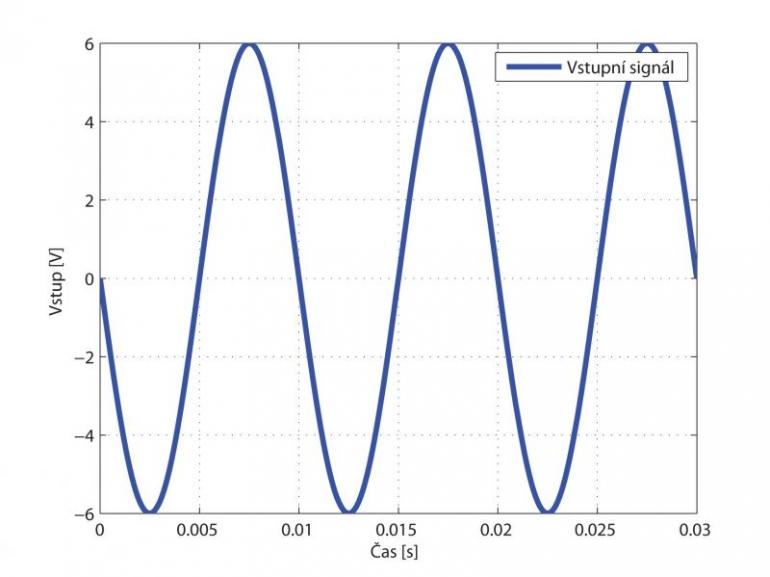

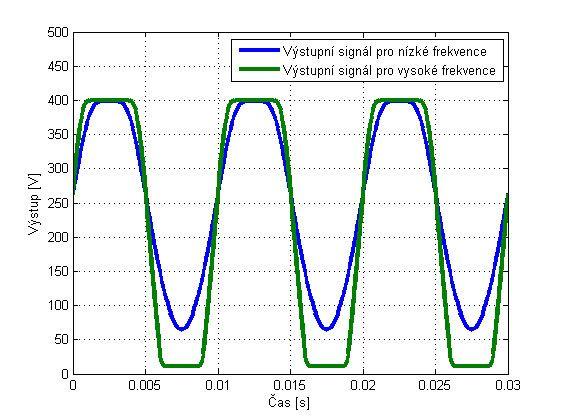
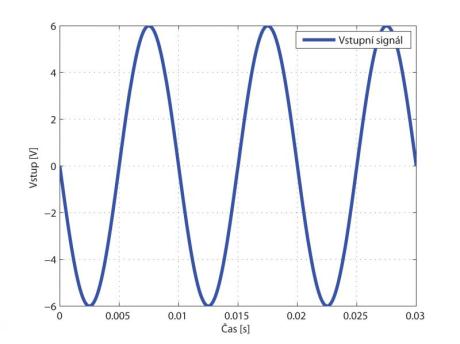
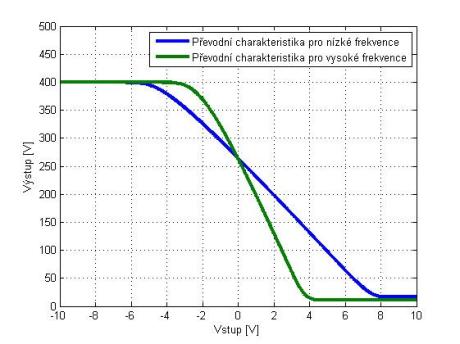
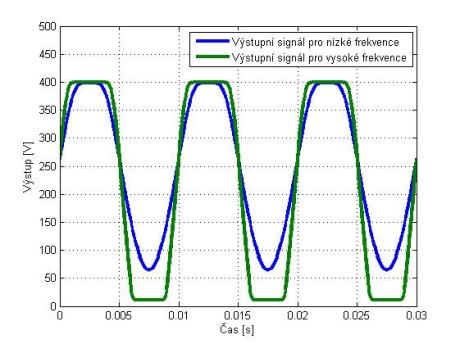
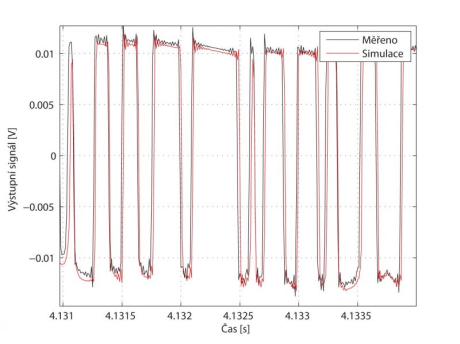
Ukázka saturace elektronkového zesilovače při různých kmitočtech
Můžeme tedy říct, že je daná vzorkovací frekvence a pro každý jeden vzorek máš jedno číslo.
Přesně tak. Samozřejmě, abychom byli schopni signál v reálném čase vůbec zpracovávat, musí jít přes vyrovnávací paměť. Tzn. že si musíme vzít vždycky nějaký úsek dat, která přijdou z převodníku, poslat si je do procesoru na zpracování, tam se příslušná čísla zmodifikují, a pak se uloží zase do výstupní vyrovnávací paměti, ze které jdou na výstupní převodník a přemění se na výsledný zvuk. Na tom procesu je důležité, jak jsou vyrovnávací paměti velké. Čím bude paměť větší, tím máme větší výhodu v tom, že bude míň operací, jako je naplňování pamětí, přepínaní procesů apod., ale současně mi bude narůstat latence (zpoždění) zpracování signálu. Samozřejmě to vždy záleží na hráči, ale musíme se pohybovat někde v rozmezí 5-10 ms.
Tohle jsem si také zkoušel, a když jsem se dostal na hodnotu cca 13 ms, tak už mi začínalo vadit, že slyším zvuk zpožděný. Jakou s tím máte zkušenost?
vstupuje Lubor Přikryl
My jsme dělali společně s VUTv Brně docela rozsáhlý výzkum, že jsme si zvali od každého nástroje několik aktivních muzikantů a zkoušeli jsme různé latence. Výsledky jsme vyhodnotili a zjistili jsme, že každý muzikant to vnímá naprosto jinak. Nicméně kytaristé jsou jedni z nejcitlivějších. Naopak nejméně citliví byli například klávesáci nebo dechaři. Těm třeba i nějakých 20 ms ještě nevadilo. Záleží také samozřejmě na stylu, jaký kdo hraje.
Ona je také pravda, že lidi jsou z toho někdy strašně vystresovaní, ale když si uvědomíš, že zvuk se šíří rychlostí těch 300 m za sekundu, tak 30 m je 100 ms, 3 m je 10 ms. No a tři metry od boxu stojíš na pódiu poměrně běžně, a už tam těch 10 milisekund zpoždění hned máš.
Datový typ definuje v programování druh nebo význam hodnot, kterých smí nabývat proměnná (nebo konstanta). Datový typ je určen rozsahem hodnot a zároveň výpočetními formulacemi, které lze s hodnotami tohoto typu provádět. (zdroj: Wikipedie)
Máme tedy vstupní signál převedený na čísla, vyřešené vyrovnávací paměti... Co následuje?
No, prakticky, když už mám nějaký signál, tak si ho můžu představit jako nějakou matematickou funkci, a pak si s tím můžu dělat cokoliv, co mi umožňuje matematika. Čili mám-li například sinusovku a chci z ní udělat obdélníkový průběh, je to úplně jednoduché. Vezměme amplitudu dané sinusovky, řekněme opět ±1,0, a já ji tisíckrát zesílím, tj. každé navzorkované číslo vynásobím tisícem, čímž dostanu amplitudu ±1000,0. A já si řeknu, že vše, co je nad 1,0, oříznu (saturuji). Takže ve výsledku dostanu signál se strmým náběhem, který se rychle dostane na hodnotu 1,0, všechny vyšší hodnoty oříznu, a pak mám zpět zase strmý přechod do 0 a dále do -1 atd. Vlastně takhle jednoduše vyrobím jiný tvar vlny. A to je základ digitálních distortionů a overdrivů. Tohle se dělá prakticky v každém zkreslovacím obvodu, v analogové oblasti funguje úplně stejný princip. Já vlastně kopíruji základní princip analogových obvodů.

Takže se tedy vlastně snažíš napodobit průběh analogových obvodů, nebo si s tím „hraješ“ tak dlouho, až se ti to prostě líbí?
Ne, já to opravdu dělám tak, že to vypočítám podle obvodů. Ale je pravda, že to „hraní si“ je historicky starší způsob. Když se dřív programovalo zkreslení, tak se dělalo přesně to, co jsem před chvílí řekl. Ale kdyby sis to poslechl, tak to moc hezky nehrálo. Znělo to spíš jak přebuzený hi-fi zesilovač. Řešilo se tedy, proč aparáty hrají lépe. A zjistilo se, že existují i nějaké frekvenční závislosti, že v klasických obvodech se obvod chová jinak na basech, jinak na výškách apod. Ten původní systém frekvenčně závislý není, takže ať do toho pouštím basové frekvence nebo vyšší frekvence, saturuje to pořád stejně. Začalo se tedy experimentovat s různými filtry zapojenými před obvodem a za ním, se zesílením a ořezáním. I toto mělo své opodstatnění.
Hezky je to vidět například u klasického elektronkového (triodového) zesilovače, kde je v katodě zapojen kondenzátor, kterým se určuje předpětí lampy, a tím, v jaké části převodní charakteristiky lampa pracuje. Kondenzátor (kapacita) je frekvenčně závislý prvek, tím je tedy daná jiná saturace na basech a jiná na výškách.
Tím bylo dosaženo hezčího zvuku a na tomhle principu byly založené první digitální zkreslovací efekty. To se bavíme o době zhruba před deseti až dvaceti léty, kdy procesory zvládaly pouze takovéhle operace - filtraci a saturaci. Moji předchůdci pak v podstatě hledali možnosti, jak tyhle algoritmy vylepšit a dosáhnout tím věrnějšího zkreslení. Například použili banky filtrů, které signál rozdělily na vyšší a nižší kmitočtová pásma, každé pásmo zpracovali zvlášť a na konci je sečetli. Prostě se snažili nějak napodobit fyzikální chování analogových předloh. Ale pořád to ještě nebyla přesná simulace obvodu zkreslení. A k tomuhle existuje paralelně, řekněme, druhá linie simulátorů elektronických obvodů, která je mimochodem už také poměrně stará. Tyto simulátory jsou opravdu velmi přesné a používají se při designu elektronických zařízení. Když se dnes navrhuje nějaký obvod, tak se nejprve poskládá model v počítači, ověří se, že je to správně zapojené, a až pak se teprve realizuje hardware. Problém je, že výpočetní náročnost je tak obrovská, že nějaké trochu složitější schéma ani dnes, se současným výkonem počítačů, nejsme schopni v reálném čase spočítat.
Ještě jsem si vzpomněl, jak ses ptal na ten chorus nebo flanger. Vždycky říkám studentům: „Vaše cena je v tom, jaké uděláte chyby. Protože kdybyste hráli úplně přesně, tak to může hrát stroj. A vy jste cenní v tom, že tam vložíte tu drobnou nepřesnost.“ Takže když vezmu chorus, jak je definovaný, je to velice jednoduchý algoritmus. Jenomže vtip je v tom, že se nikomu nelíbí, protože zní přesně tak, jako ta strojová hudba. Takže vývoj jde tam, aby zachytil všechny nedokonalosti, které se paradoxně předchozí vývoj analogové techniky naopak snažil odstranit. :-) Ale ono vlastně právě to dělá tu hudbu hezkou. Udělat čistý chorus je teoreticky jednoduché, ale nikoho to neosloví. Proto se přesně emulují analogové obvody i s rozptylem součástek, určitým drobným zkreslením, přimíchává se umělý šum... to vše do toho vnese určitou „lidskost“ a analogovou „nepřesnost“.
Když si vytvořím model lampy a zasadím ho do systému, tak to je sice technicky možné, ale je problém to použít v reálném čase?
Přesně tak. Postupy na to jsou, ale je to výpočetně strašně náročné. Ovšem skutečnost, že to nedokážeme spočítat jako celek, neznamená, že nedokážeme spočítat menší části, což je přesně směr, kterým jsme se všichni vydali. To znamená, že my si stavíme elementární bloky, které simulujeme tak, jak se má: Vezmu si obvod, podívám se, jak je zapojený, analyzuji si ho, napíšu si pár diferenciálních rovnic a snažím se je vypočítat pomocí určitých matematických postupů. A když je těch rovnic opravdu málo, třeba tři nebo čtyři, tak už jsme dnes schopni je v reálném čase spočítat se stejnou přesností jako u zmíněných simulátorů obvodů, které se používají pro design obvodů. V případě složitějšího obvodu musím uvnitř najít jednotlivé bloky, jak jsou zapojené za sebou. Pak je počítám samostatně a hudební signál v programu jde v podstatě stejně jako v daném analogovém zařízení. Tzn. projde prvním blokem, který s ním něco udělá, vstupuje do druhého bloku, kde se zase něco stane, atd. A tohle už jsme schopni spočítat.
Jiná věc bohužel je, že dělení na bloky není úplně jednoduché. Když si vezmeme nějaké klasické kytarové krabičky, kde jsou převážně operační zesilovače, tak tam je to většinou v pohodě. Jde tam o to, že výsledek následujícího bloku vyloženě neovlivňuje funkci předchozího bloku. Můžu to potom poměrně jednoduše rozdělit a výrazně mi to usnadňuje práci. Není tam navíc zpětná vazba mezi bloky. Ve složitějších zařízeních nebo zesilovačích, obzvlášť elektronkových, už to tak jednoduché, bohužel, není.
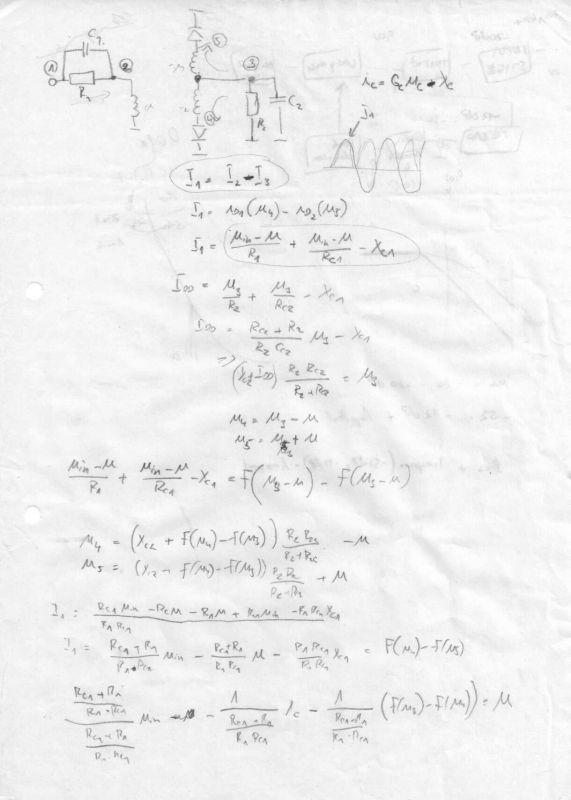
Ty rovnice vznikají jak?
Ty se dají odvodit přímo ze schématu. Když zabrousíme trochu do fyziky a matematiky, tak existují postupy, jak popsat obvod. Mám teď na mysli Ohmův zákon, Kirchhoffovy zákony a další známé formule. Z toho vznikne soustava rovnic, kterou musím vyřešit. Ovšem problém je, že vzniklá soustava je nelineární, takže řešení není triviální. Prostě nevznikne něco ve tvaru y = 2x, ale řešení hledám iterativně - tedy jako kdybych hádal. Čili nějaké odhadnuté řešení zkouším, jestli vyhovuje, a většinou samozřejmě napoprvé nevyhovuje, takže odhad trochu zpřesním a znovu zkouším, zda vyhovuje, a tak dále, dokud se k správnému řešením nepřiblížím s dostatečnou přesností. Proto je to tak náročné na výpočet. Když je nelinearita jen jedna, tak konvergence ke správnému řešení je poměrně rychlá. Když je ten obvod složitější a nelineárních funkcí je tam víc, dostaneme se do nějakého n-dimenzionálního prostoru, a tam jsou řešení kolikrát i nejednoznačná. Ale asi dost matematiky. :-)
Dobře, ale když už u té matematiky jsme, vrátím se ještě k té výpočetní náročnosti. Je problém v tom, že současná výpočetní technika je pořád ještě pomalá, a nebo se jedná o úlohy, které se nedají řešit nějakým jasným sledem kroků, neexistuje pro ně nějaký přesný postup?
Limituje nás čistě výpočetní výkon. Sekvence kroků je daná, ale je jich moc. Když si uvědomím, že pro každý vzorek, kterých je za sekundu standardně 48 000, ale interně se pracuje s daleko vyššími vzorkovacími frekvencemi, musím řešit poměrně složitý matematický problém, a tak se dostávám opravdu k limitujícímu počtu operací v procesoru.
Navíc ta povaha úlohy je svým způsobem nešťastná i v tom, že se nedá řešit paralelně na více procesorech současně. Pro výpočet každého vzorku potřebuji výsledek z toho předchozího. Takže kdybych to chtěl rozložit, tak by to teoreticky v některých případech možné bylo, ale zase by začala rychle narůstat latence. Navíc je třeba připočíst i režii spojenou s paralelizací, takže ve výsledku by to moc efektivní nebylo.
Implementace je proces uskutečňování teoreticky stanovené myšlenky nebo projektu za účelem jejího dalšího použití. Implementaci předchází analýza zadání, plánování postupu a očekávaných výsledků. Nesoulad mezi předpokladem a skutečností může být způsoben chybou implementace nebo chybou samotné metody. Správná metoda je funkční nezávisle na způsobu implementace. (zdroj: Wikipedie)
Jak pak pracuješ s tím navrženým obvodem? Pustíš do něj kytaru a zkoušíš, jak to hraje? Děláš nějaká měření, nebo to jen posloucháš? Zveš si někoho?
Nejprve si navrhnu modul, napíšu algoritmus a testuji ho na umělých signálech, které mám v počítači. To znamená, že používám sinusovku, ale klidně i nahraný kytarový riff. Ale napřed vizuálně kontroluji, jestli ten signál po zpracování vypadá tak, jak očekávám. Algoritmus je potřeba pořádně odladit, aby dělal opravdu to, co to dělat má. Přeci jen programátor je jen člověk. :-) Takže to většinou nefunguje na první pokus. Vždycky se najde nějaká chyba.
Pak to samozřejmě i poslouchám. Většinou stačí testovat jen na brnknutí. Přišel jsem na to, že neodladěné algoritmy není úplně dobré zkoušet třeba na sluchátka. Občas to může i zabolet. :-)
Když je všechno v pořádku, tak mě čeká velká řehole. Algoritmus musím přepsat do „něčeho“, v čem ho mohu vyzkoušet v reálném čase. Na to jsou ideální VST plug-iny. My na to máme už připravený vývojový plug-in, který má prázdnou smyčku pro vlastní zpracování zvuku, do které musím vepsat navržený algoritmus. Pak teprve můžu začít testovat, jak se algoritmus chová při reálném hraní - to se dost často liší od umělých a předem nahraných zvukových signálů.
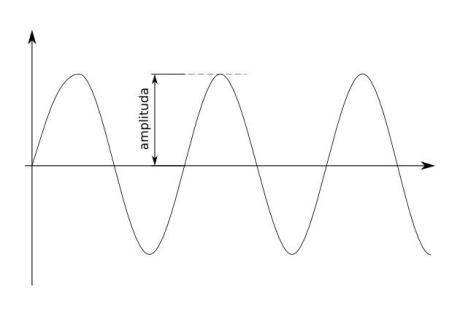
Amplituda (též výkmit nebo rozkmit) je maximální hodnota periodicky měnící se veličiny. Spolu s frekvencí, počáteční fází a u vln též vlnovou délkou je amplituda jedním ze základních parametrů periodických dějů. (zdroj: Wikipedie)
Když to hraje blbě, tak musím hledat, kde je problém, když to hraje dobře, tak si můžu pogratulovat. Pak už můžu konečně ze svého algoritmu dostat nějaké charakteristiky, které bych mohl srovnat s charakteristikami simulovaného obvodu. Můžu provést úplně stejná měření jako u analogového obvodu. Do plug-inu pustím sérii testovacích signálů s různým spektrem, abych zjistil např. frekvenční zabarvení. Pak už může konečně začít porovnávat algoritmus s analogovou předlohou. Z výsledků vidím, co je jinak, a přemýšlím, proč to tak je a co mám změnit, aby se to víc podobalo originálu. Což je tedy obrovská alchymie a je to ve výsledku třeba nějakých osmdesát procent práce vývoje algoritmu. I když pokud se budeme bavit o simulaci obvodu s „operáky“, tak tam to většinou, pokud není chyba v algoritmu, hraje stejně hned, protože zde jsou poměrně přísné normy na toleranci součástek a operační zesilovač prostě dělá to, co má. Ale například u elektronek je tolerance klidně i 20 %, a tam je zkrátka všechno jinak. Ostatně to všichni známe. Když vezmeš lampu a v aparátu ji vyměníš za jinou, tak bude hrát jinak. Ta simulace pak v zásadě nemůže být nikdy naprosto stejná, ale měl by tam být ten charakter předlohy.
Diferenciální rovnice je matematická rovnice, ve které jako proměnné vystupují derivace funkcí. Diferenciální rovnice stojí v základech fyziky a jejich aplikace najdeme ve většině oblastí lidského vědění. (zdroj: Wikipedie)
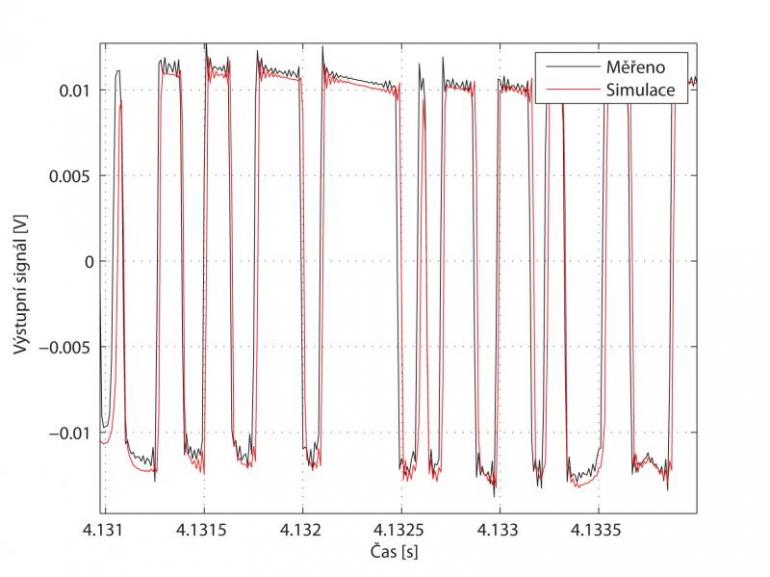
Nicméně tobě se poměrně vysoké věrnosti podařilo dosáhnout...
To je pravda. Ve své disertační práci jsem publikoval simulaci pre-ampu a potřeboval jsem doložit, že je ta simulace opravdu věrná. Musel jsem ale kvůli tomu elektronky z toho pre-ampu vytáhnout, naměřit přesně jejich charakteristiky, což byl týden měření, a získaná data jsem pak použil ve svém softwarovém modelu elektronky. Jen díky tomu jsem mohl dojít k tomu, že algoritmus hrál opravdu stejně jako předloha, což se také skutečně stalo.
Dělali jsme na to poslechové testy a naprostá většina lidí nebyla vůbec schopna poznat rozdíl. Ale musím zdůraznit, že to byl jeden konkrétní pre-amp. Když budu srovnávat s jiným preampem stejného typu, tak už to nebude pravda. Protože jsou tam jiné elektronky, jsou tam jiné rezistory (opět záleží na toleranci) atd., takže všechny pracovní body budou zase malinko posunuté a bude to hrát prostě jinak. Musí.
Slovo lineární pochází z latinského linearis, což znamená tvořeno přímkami. Obvykle slovo označuje podobnost něčeho s přímkou nebo rovností. Lineární funkce je taková funkce, jejíž hodnota na celém jejím definičním oboru rovnoměrně klesá nebo roste. Například funkce f(x) = 3x je lineární. (zdroj: Wikipedie)
Zatím se pořád bavíme o zkreslení, ale je problém simulovat i ostatní efekty? Mám na mysli např. chorus, delay apod.
To takový problém není a může to být i poměrně snadné. V podstatě i analogové krabičky jsou prakticky řešené jakoby digitálně. Najdeš tam posuvný registr, což je v podstatě digitální součástka, na vstupu je vzorkovač... Tyto efekty se simulují opravdu docela jednoduše.
Ale znáš to, zvuk obyčejného digitálního chorusu je úplně sterilní. V analogové variantě jsou opět nějaké vstupní obvody, které jsou frekvenčně závislé, často tam bývají kompresory a expandéry, aby snížily šum zpožďovací linky, na výstupu je sumační zesilovač s další frekvenční charakteristikou, a i ten BBD obvod (zpoždovací linka) není bezeztrátový, frekvenčně nezávislý. Čili pokud chci udělat věrnou simulaci chorusu, musím se všemi těmito závislostmi počítat. Opět vstupují do hry filtry, podobně jako u zkreslení. Výhodou ale je, že filtry jsou lineární obvody, takže jsou jednoduché na simulaci.
Ing. Jaromír Mačák? Ph.D.
vedoucí vývoje
Narozen v Hranicích, vystudoval Vysoké učení technické v Brně, obor Telekomunikační a informační technologie. Odborným zaměřením doktorandského studia byla digitální simulace analogových hudebních efektů v reálném čase. Během svého působení na fakultě vyučoval zpracování hudebních signálů na počítači, studiovou a hudební techniku, byl aktivním účastníkem zahraničních konferencí zaměřených na zpracování hudebních signálů, působil také na univerzitě v německém Hamburku a na brněnské JAMU.
S firmou DISK Multimedia, s.r.o., spolupracuje od roku 2007, od roku 2012 zde pracuje jako vedoucí softwarového vývoje. Je autorem algoritmů, které jsou využity pro simulaci kytarových zesilovačů a efektů. Spolupracuje také na návrhu hardwaru. Mimo to je i aktivním muzikantem. Hraje na elektrickou kytaru v kapele Tchoři.

A co třeba boxy, zesilovače...?
Ten postup je jak u boxu, tak u zesilovače v zásadě úplně stejný jako u krabiček. Samozřejmě že zvuk zkreslené kytary není jenom otázka zkreslení, ale je tam vliv i boxu a koncového zesilovače. Podle mě třeba box tvoří osmdesát procent zvuku. Takže ho do simulace musím také zahrnout. Jde jen o to, jakou metodou zvolím k simulování. Můžu použít například nějaký konvoluční algoritmus se změřenou charakteristikou boxu (to jsou ty dnes populární impulzy :-)). Je to vlastně jen dlouhý filtr, přes který signál prochází. Problém je v tom, že filtry mají ale nějaké zpoždění, což může být jedna z příčin pocitu určitého „odstupu“ zvuku od hráče.
U koncových zesilovačů musím zase provést celkovou analýzu, naměřit charakteristiky - úplně stejně jako u pre-ampů. Pouze u koncových zesilovačů je bohužel překážkou, že ho nemůžu jednoduše rozdělit na ty zmíněné bloky. Je tam vždy zpětná vazba z výstupu až úplně na vstup, takže tam to už musíme určitým způsobem obcházet.
vstupuje Lubor Přikryl
Ideální by bylo, kdyby se dala vyrobit skládačka, že by sis kteroukoliv část mohl dát analogovou a za ni si dal libovolně software. Což přesně z důvodu zmíněné zpětné vazby nejde. Kdybys mohl simulaci „useknout“, např. za koncovým zesilovačem (pak bys tam tedy musel dát nějaký naprosto nezabarvený koncový zesilovač), a připojit k tomu svůj kytarový box. A to se zkrátka nedá úplně udělat. Protože zase - mám tedy nějaký skvělý koncový zesilovač, ke kterému je připojený box, jenže reproduktor má impedanční charakteristiku, tím pádem i ten skvělý zesilovač je ovlivněný připojeným reproduktorem a zase jsme někde jinde.
Ona je velice důležitá věc, přes co muzikanti zvuk simulací poslouchají. Protože když se udělá až do konce, tak je v ní zahrnutý i reproduktor. Takže když to poslouchají např. přes kytarový aparát, už je tam jeho charakteristika vlastně dvakrát. Jinak to bude hrát zase např. na hi-fi komponentech apod. Oni si lidé pak stěžují, že jim to hraje jinak doma než ve zkušebně. Ale to ani jinak být nemůže, když to doma poslouchá na „nearfieldy“ a na zkušebně má za sebou „half stack“. Jednoduše řečeno, když už simuluji kytarový box, tak už přes něj nemůžu znovu fyzicky hrát. Je jasné, že jinak se ten zvuk někam posune.

Můžeme tedy na závěr udělat nějaké shrnutí celého vývoje?
Pravda je, že my neděláme nic, co by bylo vysloveně nové. Přesné (!) simulátory elektronických obvodů existují opravdu už desítky let. My jen hledáme způsoby, jak to zjednodušit, aby to bylo možné počítat v reálném čase. To znamená, že musíme zanedbávat určité věci, kde využíváme např. psychoakustiky.
Ale abych to tedy shrnul: Řekněme, že mám nějaké zařízení, které chci simulovat. První věc je, že si musím sehnat schéma. Ne vždy se podaří sehnat originál, takže nezbývá, než se podívat dovnitř na zapojení a překreslit jej. Naštěstí se dají dneska na internetu schémata dobře najít, ale bohužel v nich bývají chyby, kolikrát záměrně. Když mám schéma, tak se začnu dívat, co to tedy vlastně dělá, a snažím se identifikovat jednotlivé funkční bloky. Následně se pokusím bloky řešit samostatně, musím ale zároveň zohlednit všechny zpětné vazby, a popíšu je matematicky. To zatím vše probíhá ručně na papíře.
Potom si sednu k počítači a přepíšu získané rovnice do programu a napíšu algoritmus, který je umí vyřešit. Když mám návrh algoritmu hotový, tak ho začnu testovat pomocí testovacích signálů a sleduji, jestli to funguje tak, jak by mělo. Pokud ano, tak si takhle postupně připravím všechny bloky. Pak je teprve přepíšu do kódu v jazyce C, udělám si VST plug-in a začnu laborovat s vlastním zvukem a ladit obvod. To, jak jsem už řekl, trvá nejdéle, protože každá změna znamená nové měření a nové porovnání výsledků. Finální ladění probíhá pomocí poslechových testů. Používáme tzv. ABX testy, kdy do vzorku A nahraji reálný aparát, do vzorku B nahraji simulaci a vzorek X je náhodný výběr z těch dvou. Posluchač (samozřejmě neví, že A je realita a B simulace) má pak říct, jestli X je A nebo B. Může se pak pokusit identifikovat i samotné vzorky, tj. určit, který byl simulace a který skutečný aparát. Už se nám několikrát stalo, že byla takovým testováním vyhodnocena jako lépe znějící ta simulace. Což někteří testeři i těžce nesou a nechtějí tomu věřit. Jíní to zase přijmou v pohodě, že to tak prostě je. :-)
K tomu vývoji patří samozřejmě i tvorba uživatelského rozhraní, různé marketingové záležitosti apod. To by ale bylo zase na jiné povídání.
www: