Harmonie není náhoda III - kde se vzala durová stupnice?

Kde se vzala durová stupnice?
Tentokrát si ukážeme postup od přirozených násobků kmitočtu, přes tři základní harmonické funkce, k durové stupnici.
Tónika - základní harmonická funkce první
Na tónu velké C s kmitočtem 66 Hz jsme vytvořili řadu tónů přirozenými násobky s kmitočtem až 6x (či až 8x) větším. Ta řada je libozvučná a je v ní významný trojzvuk zvaný kvintakord. Náš sluch tu řadu zvládne velice lehce, pokusme se tedy doplnit ji řadami dalšími. Abychom je pak navzájem odlišili, nazveme naší první řadu tónika, můžeme ji značit písmenem T. Významný v ní bude tónický kvintakord, na obrázku 7 vlevo je naznačen tmavými notami.
Dominanta - základní harmonická funkce druhá
První dva tóny řady T jsou vzdáleny o oktávu, kmitočtově 1 : 2. Vložme mezi ně doprostřed další tón, který pak bude mít kmitočet o polovinu vyšší než základní tón, tedy 1/ f, neboli 1,5 f (lze psát jinak / f, nebo také fx 3 : 2), což bude 99 Hz. (Poznámka autora pro vážnější zájemce: prostředkem čísel 1 a 2 je zde myšlen jejich aritmetický průměr. Pišme a = 1 a b = 2 a vypočteme aritmetický průměr označený písmem x z rovnice 2x = a + b. Zdánlivě složité, ale můžete si zkusit číslo x podle rovnice vypočítat. Je to dobrý úvod pro další kroky.)
Hudebnicky řečeno bude nový tón o kvintu výš a postavíme na něm zase celou řadu kmitočtových násobků 1x až 6x. Nová řada dostala jméno dominanta, značíme ji písmenem D a opět v ní bude významný dominantní kvintakord. Tady se podíváme na obrázek 7, ve třetím taktu je tato řada vyjádřena notami.
Bez tóniky a dominanty se neobejdou snad ani ty nejjednodušší písničky.
Subdominanta - základní harmonická funkce třetí
Nyní vybereme pro třetí řadu první tón tak, že bude o třetinu výš než tón základní. Bude tedy mít kmitočet 1/ f, neboli 1,333 f (lze psát jinak / f, nebo také fx 4 : 3), což bude 88 Hz. (Poznámka autora pro vážnější zájemce: číslo 1,333 je harmonický průměr čísel 1 a 2. Počítá se podobně jako aritmetický průměr, ale s tím rozdílem, že se používají převrácené hodnoty. Označme harmonický průměr písmenem y, potom platí 2 : y = 1 : a + 1 : b. Opět si to můžete zkusit spočítat.)
Podobně utvoříme třetí řadu tónů, která dostala jméno subdominanta a značíme ji písmenem S. I v tomto případě bude významný subdominantní kvintakord. Všechny tři kvintakordy jsou na obrázku 7 zdůrazněny tmavými notami.
Zjednodušeně shrňme, k čemu jsme právě došli - dominanta kmitá o polovinu rychleji než tónika, zatímco subdominanta kmitá o třetinu rychleji než tónika.
Nyní snadno zvládnete seřadit všechny tóny těchto tří řad podle výšky do jedné řady společné. V rozsahu jednočárkované oktávy, tj. od 4f do 8f vznikne durová stupnice.
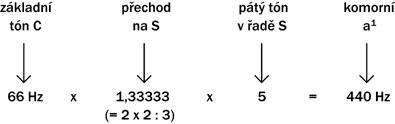
Jaké počty jsme k jejímu vzniku potřebovali? Základní kmitočet násobit prvočísly 2, 3 a 5 (i opakovaně) a dělit prvočísly 2 a 3. Například jak z velkého C odvodit kmitočet komorního a1?
Takto:
Galileo Galilei prý řekl: "Měřme věci. A když je měřit neumíme, tak se to naučme". Právě jste prošli matematikou na porozumění nejobtížnější. Ve stupnici C dur se tónický kvintakord bude jmenovat také C dur, subdominantní F dur a dominantní G dur. To je hudebníkům běžné. Jak s nimi zacházet, to ukazují učebnice hudby a především harmonie, které už vás žádnými výpočty trápit nebudou.
Přirozenou durovou stupnici lze odvodit také přičítáním a odečítáním tří intervalů: oktávy, kvinty a velké tercie. K odvození jsou i diagramy. Autor se však držel přirozených čísel, protože ta jsou všem dobře srozumitelná.
Teď už víte, že harmonie není náhoda a víte, jak odvodit durovou stupnici v přirozeném ladění. Až dojde na složitější situace, budeme muset volit mezi dvěma i více ideály, nebo dělat kompromisy. Stane se to už příště, až obrátíme pozornost k vedlejším harmonickým funkcím, k mollovým akordům v durové stupnici.
Doplňková literatura:
Stanislav Pavilek: Stručný přehled všeobecné hudební nauky
Jaroslav Kofroň: Učebnice harmonie
Juan G. Roederer: Physikalische und psychoakustische Grundlagen der Musik