Harmonie není náhoda I - proč ladí (kvint)akord? (1)
Proč ladí (kvint)akord? (1)
Přitažlivá slova: harmonie, souzvuk, soulad... Něco příjemného pro naše smysly i city. Souzvuk můžeme vychutnat a ocenit tím víc, když jsme zažili také nesouzvuk, ať už ve vztazích mezi lidmi nebo v hudbě.
Zpěv nebo komponování nám jde snadno, když nepotřebujeme žádná pravidla a orientuje nás dobře vyvinutý cit, který hodně záleží na naší zkušenosti (hodně jsme toho už slyšeli, zahráli a zazpívali) a také na zkušenostech tisíců generací našich předků, "zapsaných" do citů, které jsme zdědili. Něco nás však žene dál do neznámých krajin, hledat nové melodie a nové styly. Ocitneme-li se v neznámé krajině, můžeme směr určit podle polohy slunce či podle kompasu, to už si ale trochu pomáháme znalostmi, rozumem... Dokonce i v umění nám výrazně může pomoci rozum.
Vzpomeňme známý případ z malířství, nad kterým žasl celý svět: záhadný úsměv Mony Lisy. Před jejím obrazem si kavalíři stříleli kulky do hlavy. Magie? Ona se na vás z dálky usmívá, ale když přistoupíte blíže, výraz se jakoby změní. Autor Leonardo da Vinci byl nejen umělcem, ale i vědcem a podpořil svým věděním citové působení. Zkoumal stavbu lidského těla (v obličeji je asi 40 svalů, které signalizují naši náladu). Také už věděl, že v některých barvách rozlišujeme detaily lépe, tedy z větší dálky než v barvách jiných. Když tedy tvar úst namaloval v jedné barvě a kolem stíny v odlišném barevném tónu, docílil ohromujícího efektu.
I pro hudebníka bývá rozum velmi dobrým pomocníkem citu. Říká se, že matematici bývají dobří hudebníci. Pomáhají jim totiž dost jednoduché počty.
Hudba je založena na harmonii a já vám v několika článečcích chci stručně ukázat, na čem stojí, ukázat základy, které často zůstávají skryty. Už dávno mě napadla otázka: Kde se vzala durová a kde mollová stupnice? A jeden znalec mi nedávno nasadil brouka do hlavy: Čím to je, že mollový kvintakord je jakoby obrácený durový, symetrický k durovému? Když jsem odpovědi našel v knihách, hovorech s odborníky i ve své rozumem podpořené fantazii, bylo to, jako když se zvedne tajemná mlha a okolí se rozjasní ve sluneční záři.
Potěšení smyslů
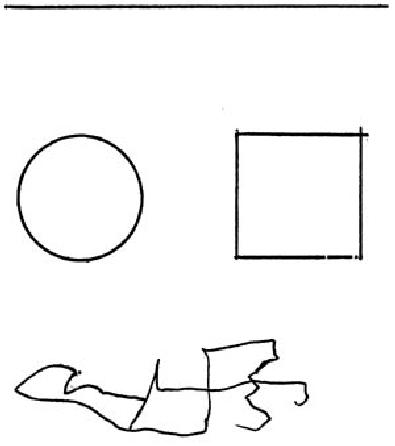
Magická moc hudby je založena na tom, co platí pro vše živé: Příliš jednoduché podněty nudí, mírně složité a mírně obtížné zaujmou a povzbudí, a když je člověk zvládá, cítí potěšení. Příliš složité podněty a nároky vedou ke stresu a únavě, dokonce k rezignaci a odmítnutí. Podíváte-li se na obrázek č. 1, které verze vám budou sympatické? První verze a, ani poslední d asi nejsou nijak přitažlivé. Příjemně působí ty, které jsou mírně složité, tvořeny podle jednoduchých pravidel, tedy nejspíš b a c.
Také předmětem hudby jsou především pravidelná slyšitelná kmitání, tj. tóny. Je-li jich víc (jeden by nás nudil), ať už současně znějících nebo jdoucích po sobě, potěší nás, budou-li vzájemně v jednoduchém až mírně složitém vztahu. Ta nejdůležitější vlastnost tónu je rychlost kmitání a budeme si tedy všímat vztahu této rychlosti u různých tónů.
Tón a kmitočet
Tón "komorní a" kmitá 440krát za vteřinu. Budeme psát f= 440 Hz. Písmeno f je zde zkratkou latinského slova frequentia - česky kmitočet. Hz je zkratkou jména fyzika Hertze, jména užívaného pro kmit za vteřinu.
Jestliže druhý tón bude kmitat dvakrát rychleji, tj. f = 880 Hz, bude pro hudebníka o oktávu vyšší, tedy "dvakrát čárkované a". Poměr kmitočtů 1 : 2 je vztah tak jednoduchý, že pro označení obou tónů používáme stejné písmeno a. Když jsou zpívány současně, někteří autoři takový zpěv dokonce označují za jednohlasý. Zpíváme-li je střídavě, můžeme říci, že přeskakujeme do fistule.
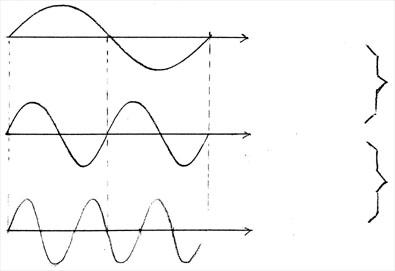
Druhý obrázek ukazuje, jak se tóny o různém kmitočtu zobrazí na osciloskopu nebo na černé gramofonové desce. (Pro důkladnější zájemce poznamenejme, že fyzik by tyto vlny nazval "časový průběh akustického tlaku", a že jde o tvar kmitů matematicky nejjednodušší, to jest "sinusové".)
Zatímco průběh nahoře, označený 2a, kmitne jednou, prostřední 2b dvakrát a dolní průběh 2c za stejný čas kmitne třikrát. Poměr 1 : 2 : 3 je zvolen úmyslně, posluchači takové tóny hrané buď současně nebo po sobě, budou znít libozvučně. Jsou navzájem v jednoduchém kmitočtovém vztahu.
Buďme konkrétnější a zvolme kmitočet průběhu 2a 66 kmitů za vteřinu (to znamená, že trvání jednoho kmitu je šestašedesátina vteřiny). Pišme f= 66 Hz. Jde o kmitočet tónu velké C v čistém ladění. Kmitočty těch dalších snadno spočítáte.
Poměr kmitočtů 1 : 2 (a také 2 : 1) je příznačný pro interval "oktáva". Jméno dostal, až byla hotova celá stupnice. Tu odvodíme později. Poměr kmitočtů ze středního (2b) a dolního (2c) obrázku je 2 : 3 a tento interval dostal jméno "kvinta". Vyšší tón v kvintě kmitá o polovinu rychleji, než tón nižší. Neboli 1,5krát rychleji. (Poznámka: Pythagoras navrhl tvořit řadu tónů, stupnici, která vznikne pouze pomocí oktáv a kvint. Můžeme mluvit o Pythagorejském ladění.)
Tolik na začátek. Příště si ukážeme další konsonantní, čili souzvučné intervaly a nejdůležitější akord, durový kvintakord. Pak už nebude daleko k durové stupnici.
Ať se vám dobře hraje.
Literatura:
Compendium Musicae Renati Cartesii
Doc. Jan Obdržálek: Hudební akustika